Initially the orientation points along the negative z-axis: View Direction (0|0|-1), Right Vector (1|0|0), UpVector (0|1|0).
Let's say, RotateY is called. This does no longer mean that the orientation is rotated around the y-axis. Instead, it is rotated around the up vector.
But what does it mean to rotate the "orientation"? It means to rotate the view direction, the right vector and the up vector. Rotation around a certain straight line is normally done by multiplying the vector with a rotation matrix. I already had started to implement this kind of rotation, but then I realized that we have a very special case here which can be handled more easily:
This makes our case special:
- only two vectors must be rotated at each RotateX/Y/Z
- all vectors are perpendicular, so one vector always can be computed by the cross product (i.e. we have to rotate only one vector!)
- the vector which must be rotated around the straight line is perpendicular to the line's direction
- we know the vector which is perpendicular to the vector which must be computed and the line's direction
Let's assume we want to rotate the camera's orientation around the right vector. This means, that the right vector will not change (1). As point (2) says, it is enough to rotate the view direction vector. The new up vector can be computed by the cross product (we could also rotate the up vector and calculate the view direction vector - it would create the same result).
If you wonder what I need the last two points for, this image might help:
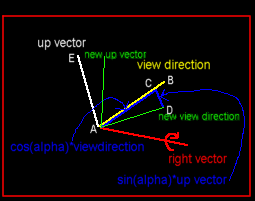
The view direction is rotated around the right vector. The angle is called alpha and this alpha is negative, so the sine "sin(alpha)" is negative, too.
If you know want to rotate the view direction vector, you first shorten it to the upper blue line (AC). This vector is cos(alpha)*viewdirection (where viewdirection is a vector).
Now you have to add the vector from C to D which is parallel to the upvector, because the upvector is perpendicular to rightvector and view direction.
Look at this image, where we have the same situation in 2d:
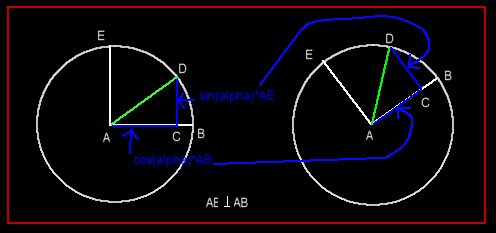
Here you can see clearly that the new vector (AD) is:
AD = cos(alpha)*AB+sin(alpha)*AE.
It is the same in 3d!
You now can turn a vector around another one (at least in our special case). After you have turned the view direction around the right vector, you can compute the up vector by using the cross product - ready!
The rest is easy to understand:
The new orientation is computed each time a Rotate? method is called. As it is always only one rotation, it does not require too much calculation time.
The Move (or Strafe) methods are also very easy: Simplify stretch the right vector / up vector / view direction vector with a certain factor and add this vector to the position.
If you have problems to imagine how the three orientation vectors behave, you can have a look at the sample code Looking at the camera. Here you can use the same keys to control the camera. But the camera is not used for rendering - you can see the three vectors: right vector (red), up vector (white), and view direction vector (yellow):